Research Projects
Here you can find brief descriptions and references for the various research projects I have been/am currently a part of.
Current research
Rankings in multi-body competitions
The 20th century saw dramatic strides in social choice theory and the problem of rankings, i.e., of computing some coherent ranking on a set of alternatives given a collection of individual preferences that may, in the aggregate view, conflict with each other. One model tackling this ranking computation is the Plackett-Luce model, an extension of the famous Bradley-Terry model into preferences among more than two alternatives at a time. We extend recent work on efficiently calculating rankings in the Bradley-Terry model to the Plackett-Luce model, thus allowing scalable ranking computations when preferences are made among an arbitrary number of alternatives.
References:
Past research
Community detection in hypergraphs
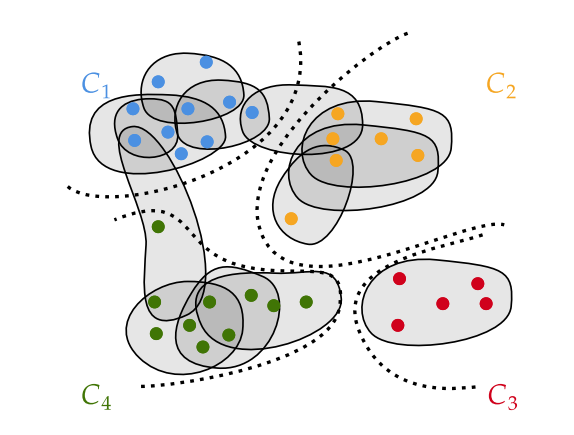
Community detection in graphs is known to be related to a graph compression problem such as described by Rosvall and Bergstrom in their paper “An information-theoretic framework for resolving community structure in complex networks.” We extend their framework to the hypergraph setting, so that we can partition the nodes of a hypergraph into communities such that the community structure is maximally informative of the underlying hypergraph structure.
References:
Multiplex reconstruction
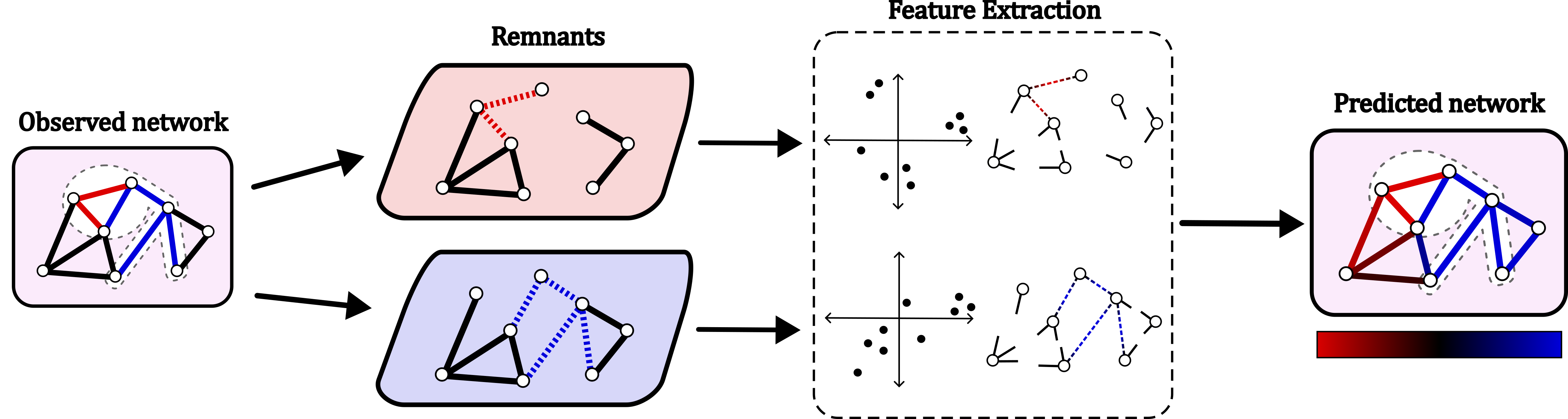
Multiplex networks extend classical network theory by allowing for the same set of entities to interact in a variety of ways. Observing multiplex structures directly is not always an easy task, however, and is prone to a variety of errors. One such observation error that does not have an analogy in classical network theory is a failure to observe the type of interaction, merely its existence in some layer. We develop a framework to infer the most likely multiplex structure given some partial observations of the full multiplex structure and observation of the aggregate topology.
References: